To understand what Rayleigh-Taylor Flow is, it is easiest to start with an example, something common. Take a container filled with oil and water. The two liquids have different densities and the oil floats on top of the water. Now assume you started with the water on top of the oil and let them mix. What you would see is a sinusoidal, or egg crate shape, pattern of waves forming along the interface.

This pattern of the fluids mixing is known as Rayleigh-Taylor flow (name to be explained later) and it is highly complicated. Although mixing oil and water is fun to watch, the specific combination of these two fluids doesn’t have too many applications in real life. However, Rayleigh-Taylor flow performs similarly in any combination of fluids or gases playing a crucial role in nuclear fusion, supernovas, volcanoes, and even simple weather patterns.

The basics of Rayleigh-Taylor flow is that there is a heavy fluid moving into a light one, ie – water moving into oil. As they mix, the interface changes due to a system of vortices that occurs. If you zoom into the inflection point of the sinusoids from a 2D point of view, you would see the following reaction:

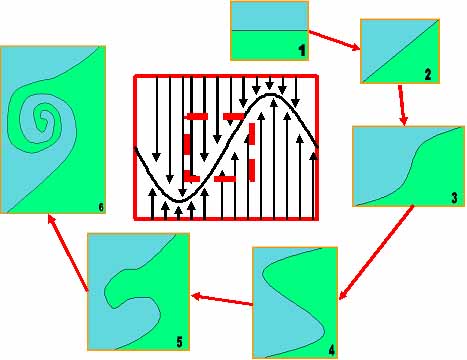
As you can see, as the fluids move into one another, a vortex occurs at the inflection point. This vortex is caused because of the frictional forces occurring due to the viscosity of the fluids.

Over time, this vortex interacts with the rest of the fluid and a “mushroom” effect occurs. This process is hard to describe, but easy to show. The following picture is courtesy of physicist Dr. Andrew Cook, physicist at LLNL:

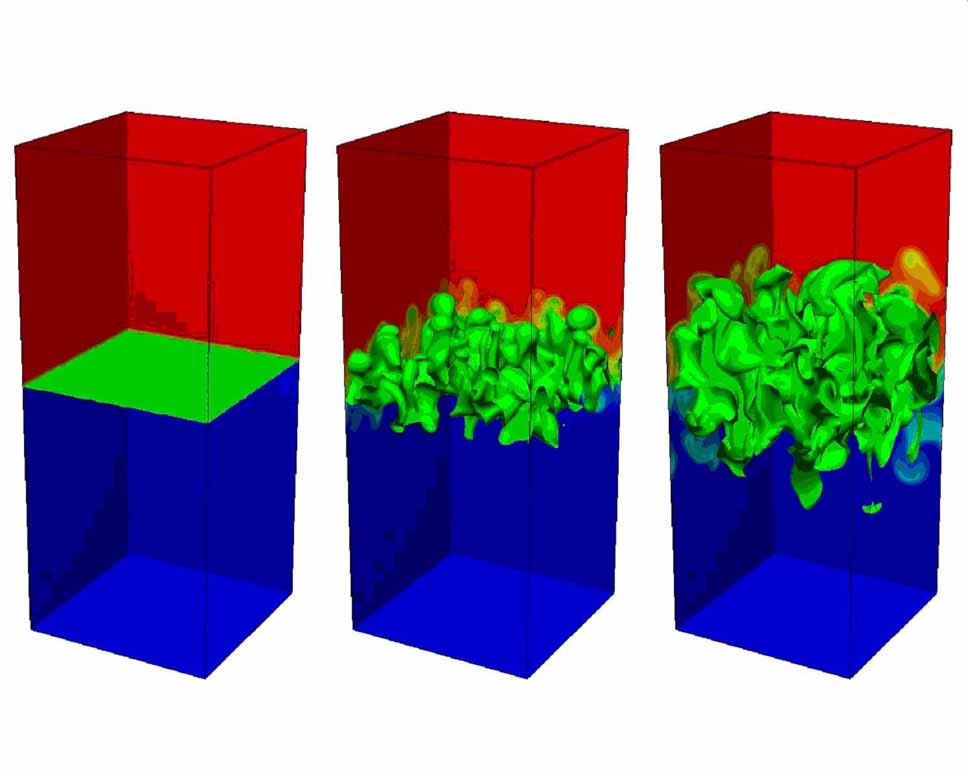
Dr. Cook created these images through CFD modeling and uses them for his research in nuclear fusion.

In the 1880’s Lord Rayleigh observed the two fluid mixture seen above and concluded that it occurs due to the gravitational forces. In 1950 Sir Geoffrey Taylor realized that it was not just forces due to the effect of gravity, but all acceleration. Hence, the effect took on the name “Rayleigh-Taylor flow” or “Rayleigh-Taylor instability”.

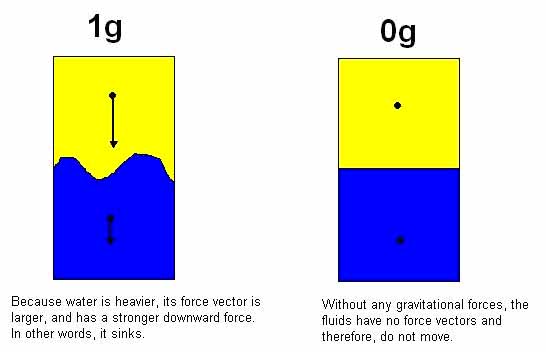
Now, return back to our container with water on top and oil on bottom. Because water is heavier than oil, the water will fall, however in a zero gravity environment, the fluids won’t move because there are no external forces acting on them. Consider the following free body diagram:

Sir Isaac Newton and his apple have shown us that gravity makes things fall, likewise, without gravity, things don’t fall. So go back to the oil/water container in zero gravity. Now imagine you move this container straight down in the direction of the arrow above. Because you’re now moving the container down, the water moves to the top of the container. In this case, you’re applying a negative g-force. Depending on how fast you move the container, the Rayleigh-Taylor flow will occur differently. Refer to the following diagram:

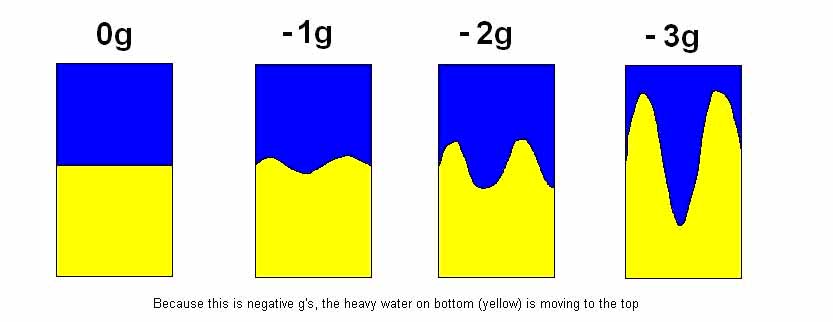
If you move the container really quickly, the eddies will be large; if you move the container slowly, the eddies will be small. The question is, how do you accelerate the container so that you know exactly how large the eddies will be after a certain amount of time? And then, once you know, how will you control it?

Well, the first step of the process is understanding how Rayleigh-Taylor flow works. The rate at which you are moving the container can be transferred into an acceleration profile. For instance, lets say you wanted to move the container so that you create a force equal to gravity. Well, return to your basic equations…..

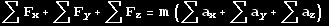
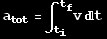
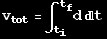
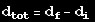
First time seeing Newtonian physics? No worries. Basically, Newton claimed that a force is mass times acceleration:

Force=mass*acceleration

This means that the force is equal to gravity is an objects mass times how fast it will fall. If you wanted to create a force twice as much as gravity, accelerate the object twice as fast. This is Newton’s 2nd Law, tell your teacher, they’ll be impressed that you know. Do heavier objects fall faster than light ones? Ask Mr. Galileo Galilei.

Now think about how things move….hmmm…tough to explain….here’s a website!

SO, lets go back to the container. Assuming you wanted to move it so that you created a force equal to gravity, you would need to apply a constant, 1g force. The acceleration profile associated with the constant 1g force is as follows:

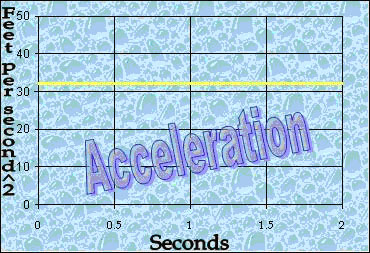
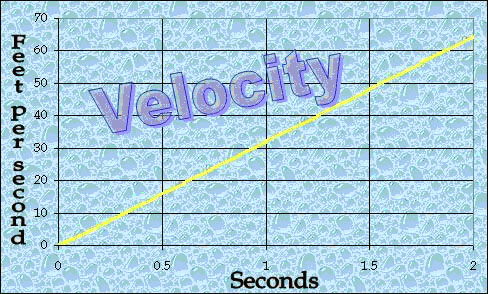
So, if this is the acceleration profile, the velocity profile looks like this:

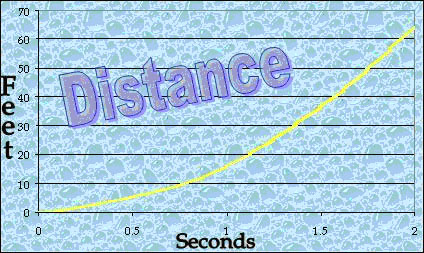
And its distance profile looks like this:

HAZAAH!! Newtonian physics!!

Now, just to make things complicated, we (G-Dawgs) want to test an acceleration profile that looks like this: